一、生物进化理论和遗传学基本知识
- 达尔文的自然选择学说
- 遗传:子代和父代具有相同或相似的形状,保证物种的稳定性;
- 变异:子代和父代、子代不同个体之间总有差异,是生命多样性的根源;
- 生存斗争和适者生存:具有适应性变异的个体被保留,不具有适应性变异的个体被淘汰。
- 达尔文自然选择学说认为:
- **遗传和变异是决定生物进化的内在因素。**遗传——保持物种的特性;变异——使物种适应新环境而不断向前发展。
- **遗传物质的载体是染色体。**染色体是由DNA和蛋白质两种物质组成的。
- **基因,染色体上具有控制生物形状的DNA片段。**一条染色体含有一个DNA分子,一个DNA分子上有许多个基因。基因存储着遗传信息,可以准确复制,也能发生突变。
- 生物遗传和进化的规律
- 染色体由基因构成,决定了生物的形状;
- 生物所有遗传信息包含在染色体中;
- 同源染色体的交叉或变异生成新的物种,使生物呈现新的形状;
- 适应能力强的基因或染色体,有更多的机会遗传到下一代。
二、遗传算法概述
- 该算法是根据大自然中生物体进化规律设计提出的。
- 是一种通过模拟自然进化过程搜索最优解的方法。
- 该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。
- 在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快获得较好的优化结果。
- 应用领域
- 函数优化:非线性、多模型、多目标的优化问题
- 自动控制:控制器参数的优化
- 机器人:路径优化
- 图像处理:图像处理过程中的特征提取、图像分割等的优化计算
三、遗传算法中的基本概念
- 个体:模拟生物个体,即可行解,对应染色体。
- 种群(population):模拟生物种群,由若干个体组成,即可行解集。
- 染色体(chromosome):可行解的编码表示(二进制编码)。比如:个体9对应染色体1001。可行解编码的分量,成为基因(gene),01。当然,也可以通过实数编码。
- 适应度(fitness):生物个体对环境的适应能力。
- 适应度函数(fitness function):遗传算法用来评价个体(解)优劣的数学函数。通常情况下,适应度函数值越大,解的质量越好。
四、遗传操作
1 选择
遗传算法使用选择运算实现对个体进行优胜劣汰操作:
- 适应度高的个体被遗传到下一代群体中的概率大;
- 不产生新个体。
经典的选择算子采用轮盘赌选择方法。 轮盘赌选择的基本思想是:个体被选中的概率与其适应度函数值大小成正比。设种群大小为 𝑛 ,个体 𝑖 的适应度为 𝐹𝑖 ,则个体 𝑖 被选中遗传到下一代群体的概率为: $$ 𝑃_𝑖=\frac{F_i}{\displaystyle \sum^{n}_{i = 1}F_i} $$ 例:假设有以下种群[16, 2, 8, 4, 1],设个体值即为适应度值,可得选择概率和累积概率。轮盘赌选择可表示为:随机生成一个0~1的数,该数从上往下第一个小于的累积概率对应的个体,即为选择的个体。
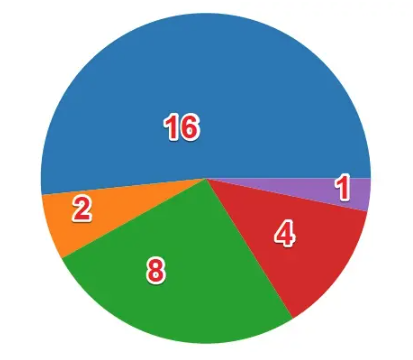
| 个体 | 适应度 | 选择概率 | 累计概率 |
|---|---|---|---|
| 16 | 16 | 0.516 | 0.516 |
| 2 | 2 | 0.065 | 0.581 |
| 8 | 8 | 0.258 | 0.893 |
| 4 | 4 | 0.129 | 0.968 |
| 1 | 1 | 0.032 | 1 |
import numpy as np
s = [16, 2, 8, 4, 1] # 5个个体
s_p = list(map(lambda x: x / sum(s), s)) # 选择概率
r = np.random.random() # 0-1之间的随机数
m = 0
c = 0
for i in range(len(s)):
m += s_p[i] # 求累积适应度
if r <= m:
c = i
break
print(s[c])
也可以有其他选择的方式,如随机选择。
def selection(pop):
sum_fitness = 0 # 适应度总和
for i in range(len(pop)):
sum_fitness += pop[i].fitness
pop_new = [pop[0]] # 假定pop[0]是最优个体,保留
while len(pop_new) < len(pop): # 基于轮盘赌的复制操作,直到复制到原始种群规模
r = np.random.random()
m = 0
for i in range(len(pop)):
m += pop[i].fitness / sum_fitness
if r <= m:
pop_new.append(pop[i])
break
return pop_new
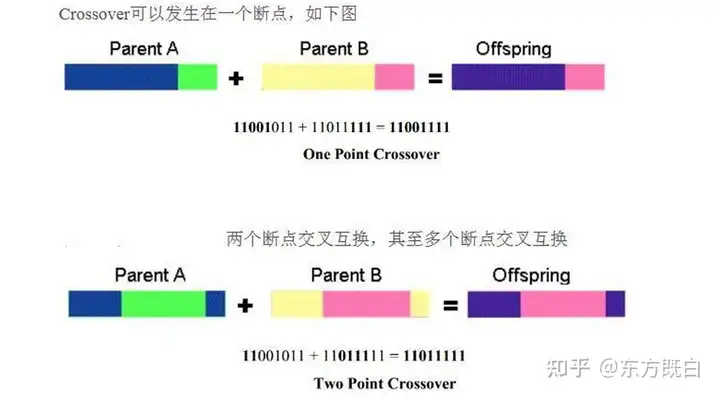
2 交叉
互换两个染色体某些位上的基因,是产生新个体的主要方法。
例1:设染色体S1=01001011,S2=10010101,交换其后4位基因,得S1’=01000101,S2’=10011011
例2:设个体1值为10,个体2值为20,按照2:8交叉,交叉后个体个体1′=10∗0.2+20∗0.8=18 , 个体个体2′=10∗0.8+20∗0.2=12
可以发生在一个断点或者多个断点。
def crossover(pop):
for i in range(1, len(pop), 2): # 0处最优个体保留
p = np.random.random()
if p < Pc and len(pop) > i + 1: # 两两交叉
cross_range = np.random.random()
pop_i = pop[i].x
pop_j = pop[i + 1].x
pop[i].x = pop_i * cross_range + pop_j * (1 - cross_range)
if fitness(pop[i].x) < fitness(pop_i): # 保留子代和父代中的最优个体
pop[i].x = pop_i
pop[i + 1].x = pop_j * cross_range + pop_i * (1 - cross_range)
if fitness(pop[i + 1].x) < fitness(pop_j):
pop[i + 1].x = pop_j
pop[i].fitness = fitness(pop[i].x)
pop[i + 1].fitness = fitness(pop[i + 1].x)
return pop
3 变异
改变染色体某个(些)位上的基因。
例1:染色体S=11001101,第三位发生变异,得S’=11101101
例2:实数编码,个体值为10∈[0, 100],发送变异,即再随机生成一个数,如59。
def mutation(pop):
pop_new = [pop[0]] # 0处最优个体保留
for i in range(1, len(pop)):
p = np.random.random()
ind = Individual()
if p < Pm: # 0-1随机数 小于 变异概率,则进行变异
ind.x = Xx + (Xs - Xx) * np.random.random() # 重新生成定义域内的一个随机数
ind.fitness = fitness(ind.x)
pop_new.append(ind)
else:
ind.x = pop[i].x # 大于等于 变异概率,不改
ind.fitness = pop[i].fitness
pop_new.append(ind)
return pop_new
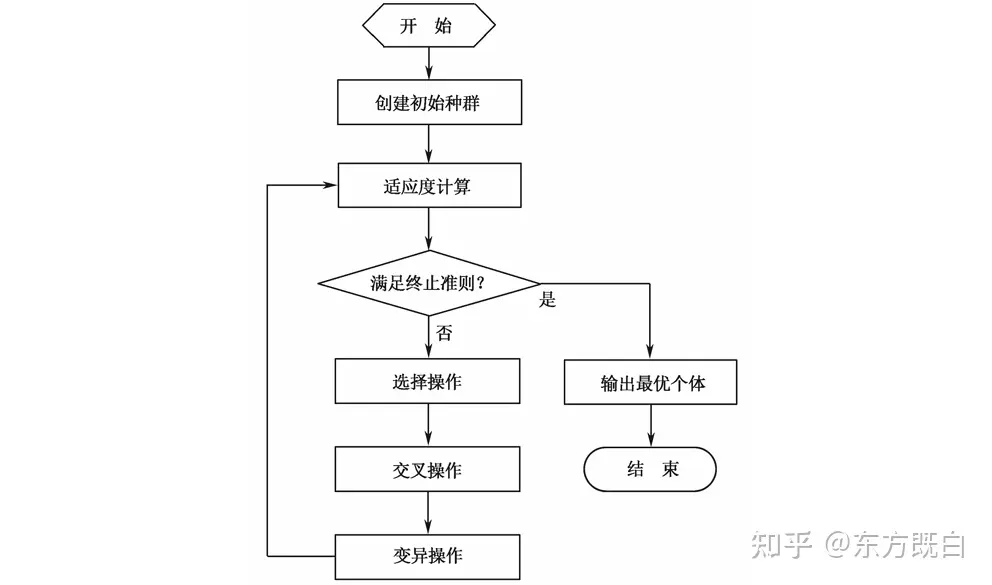
五、遗传算法步骤
- 初始化个体与种群;
- 对优化问题的解进行编码——实数编码/二进制编码;
- 个体评价,适应度函数的构造与应用;
- 遗传操作:选择、交叉、变异;
- 终止条件判断,不满足终止条件则转3。
六、Python实现
求解f = x +10* sin(5* x)+7* cos(4* x)在[0, 10]上的最大值。
import numpy as np
from matplotlib import pyplot as plt
NP = 50 # 种群数量
Pc = 0.8 # 交叉率
Pm = 0.1 # 变异率
G = 20 # 最大遗传代数
Xs = 10 # 上限
Xx = 0 # 下限
def fitness(x):
return x + 10 * np.sin(5 * x) + 7 * np.cos(4 * x)
# 个体类
class Individual:
def __init__(self):
self.x = 0 # 染色体编码
self.fitness = 0 # 个体适应度值
def __eq__(self, other):
self.x = other.x
self.fitness = other.fitness
# 初始化种群
def init_population(pop, N):
for i in range(N):
individual = Individual() # 个体初始化
individual.x = np.random.uniform(Xx, Xs) # 个体编码,0~10正态分布
individual.fitness = fitness(individual.x) # 计算个体适应度
pop.append(individual)
# 选择:基于轮盘赌的复制操作
def selection(pop):
sum_fitness = 0
for i in range(len(pop)):
sum_fitness += pop[i].fitness
pop_new = [pop[0]]
while len(pop_new) < len(pop):
r = np.random.random()
m = 0
for i in range(len(pop)):
m += pop[i].fitness / sum_fitness
if r <= m:
pop_new.append(pop[i])
break
return pop_new
# 交叉
def crossover(pop):
for i in range(1, len(pop), 2):
p = np.random.random()
if p < Pc and len(pop) > i + 1:
cross_range = np.random.random()
pop_i = pop[i].x
pop_j = pop[i + 1].x
pop[i].x = pop_i * cross_range + pop_j * (1 - cross_range)
if fitness(pop[i].x) < fitness(pop_i):
pop[i].x = pop_i
pop[i + 1].x = pop_j * cross_range + pop_i * (1 - cross_range)
if fitness(pop[i + 1].x) < fitness(pop_j):
pop[i + 1].x = pop_j
pop[i].fitness = fitness(pop[i].x)
pop[i + 1].fitness = fitness(pop[i + 1].x)
return pop
# 变异
def mutation(pop):
pop_new = [pop[0]]
for i in range(1, len(pop)):
p = np.random.random()
ind = Individual()
if p < Pm:
ind.x = Xx + (Xs - Xx) * np.random.random()
ind.fitness = fitness(ind.x)
pop_new.append(ind)
else:
ind.x = pop[i].x
ind.fitness = pop[i].fitness
pop_new.append(ind)
return pop_new
# 遗传算法
def gene_algorithm():
pop = []
init_population(pop, NP)
best = sorted(pop, key=lambda pop: pop.fitness, reverse=True)[0] # 最佳点
pop[0] = best
for k in range(G):
pop = selection(pop)
pop = crossover(pop)
pop = mutation(pop)
best = sorted(pop, key=lambda pop: pop.fitness, reverse=True)[0] # 最佳点
pop[0] = best
print(best.fitness)
return pop
if __name__ == "__main__":
pop = gene_algorithm()
# 绘图
x = np.linspace(Xx, Xs, 100000)
y = fitness(x)
scatter_x = np.array([ind.x for ind in pop])
print(scatter_x)
scatter_y = np.array([ind.fitness for ind in pop])
best = sorted(pop, key=lambda pop: pop.fitness, reverse=True)[0]
print('best_x', best.x)
print('best_y', best.fitness)
plt.plot(x, y)
plt.scatter(scatter_x, scatter_y, c='r')
plt.scatter(best.x, best.fitness, c='g', label='best point')
plt.legend()
plt.show()
